こんにちは。塾長のFです。
今日は運動学のてこや運動法則、運動の面や軸の問題を作ってみました。
運動学は難しく苦手な人が多いですが、しっかりコツを抑えていきましょう。
立位姿勢とは?
問題1 基本的立位姿勢でないのはどれか。【難易度☆】
1.顔面を正面に向ける。
2.前腕を回外位にする。
3.下肢を平行にする。
4.踵を密着させる。
答えと解説をみる
答え
2
立位姿勢は2種類あります。
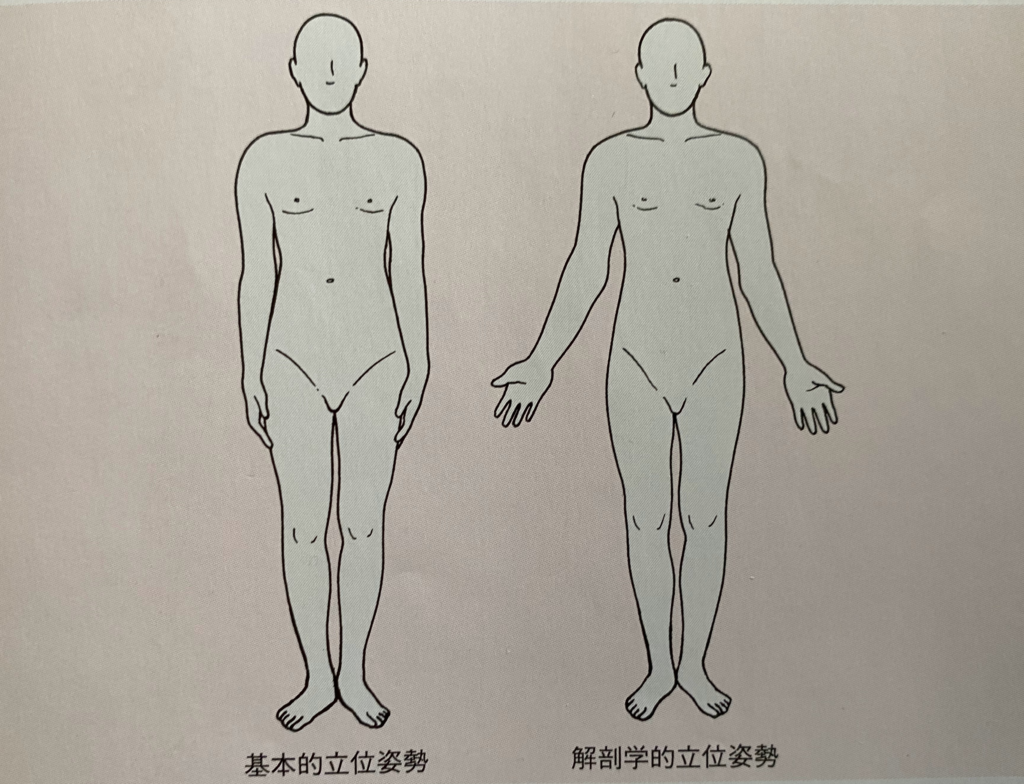 基本姿勢
基本姿勢
| 基本的立位姿勢 | 解剖学的立位姿勢 |
| 顔 面 | 正 面 | 正 面 |
| 上 肢 | 下 垂 | 下 垂 |
手 掌
(前腕) | 中間位 | 回外位 |
| 下 肢 | 平 行 | 平 行 |
| 踵 | 密 着 | 密 着 |
| つま先 | 軽く開く | 軽く開く |
運動の面と軸の関係
問題2 運動の面と軸で正しい組合せはどれか。【難易度☆☆】
1.垂直軸 ― 前腕回内
2.矢状面 ― 肩関節外転
3.前頭軸 ― 頭部側屈
4.水平面 ― 膝関節屈曲
答えと解説をみる
答え
1
| 運動面 | 運動軸 | 基本運動 |
| 矢状 面 | 前頭 軸 | 屈曲、伸展 |
| 前頭 面 | 矢状 軸 | 外転、内転 |
| 水平 面 | 垂直 軸 | 外旋、内旋 |
上記の運動面、運動軸は「解剖学的立位姿勢」がベースになっています。
面と軸は必ずセットで覚えましょう。
1.前腕の回内・回外は、水平面-垂直軸上の運動で、「内旋・外旋」に該当します。
2.肩関節の外転・内転は、前頭面-矢状軸の運動です。
3.頭部の側屈は、前頭面-矢状軸の運動で、「内転・外転」に該当します。
4.膝関節の屈曲・伸展は、矢状面-前頭軸の運動です。
ベクトル量とスカラー量
問題3 ベクトル量には含まれず、スカラー量のみに含まれるのはどれか。【難易度☆☆】
1.力
2.運動量
3.質 量
4.大きさ
答えと解説をみる
答え
3
ベクトルとスカラーはともに物理学における概念で、世の中にある色々な「量」をベクトルとスカラーとに分ける考え方です。
ベクトルとスカラーの違いは、方向をもつかもたないかです。
ベクトル量は、大きさ+方向を持つ量のことです。力、速度、加速度、運動量、力積など。
スカラー量は、大きさのみを持つ量のことです。長さ(身長など)、温度、質量(体重)など。
例えば、「身長は斜め45度の170cm」とか「体重が水平方向に60kg」なんて言い方しませんねw
| ベクトル量 | スカラー量 |
| 含まれる概念 | 大きさ
方向 | 大きさ |
| 具体例 | 力
速 度
加速度
運動量
力 積 | 質 量
温 度
長 さ |
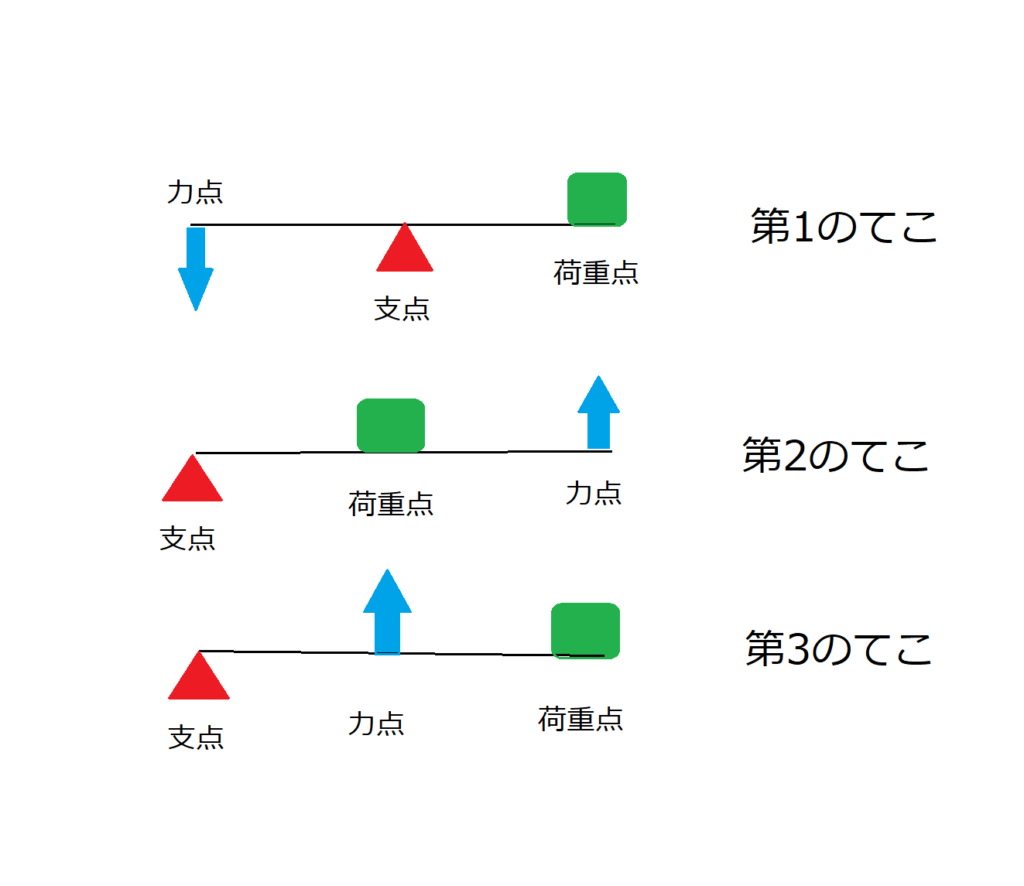
てこの種類
問題4 誤っている組合せはどれか。【難易度☆☆】
1.中殿筋による片足立ちでのつりあい ― 第1のてこ
2.ハムストリングスによる膝屈曲 ― 第2のてこ
3.下腿三頭筋によるつま先立ち ― 第2のてこ
4.上腕二頭筋による肘屈曲 ― 第3のてこ
答えと解説をみる
答え
2
第1のてこ(安定性のてこ)
【特 徴】
・安定性、シーソー
・支点が力点と荷重点の間にある。
【身体での具体例】
1)頸部伸筋群による頭部のつり合い
2)中殿筋による片足立ちでのつり合い
3)上腕三頭筋による肘伸展
第2のてこ(力のてこ)
【特 徴】
・小さな力で大きな荷重に対抗できる。
・力の腕の長さが荷重の腕の長さより長い。
*力の腕の長さ=支点から力点までの長さ
*荷重の腕の長さ=支点から荷重点までの長さ
・荷重点が支点と力点の間にある。
・人体での例は少ない。
【身体での具体例】
1)腕橈骨筋による肘屈曲
2)下腿三頭筋によるつま先立ち
3)舌骨上筋群による下顎骨の開口運動
第3のてこ(運動のてこ)
【特 徴】
・運動の速さに対して有利。力では不利。
・力の腕の長さが荷重の腕の長さより短い。
・力点が支点と荷重点の間にある。
・人体での例が多い。
【身体での具体例】
1)上腕二頭筋による肘屈曲
2)ハムストリングスによる膝屈曲(腹臥位)
3)三角筋による肩外転
運動の法則
問題5 運動の法則で誤っているのはどれか。【難易度☆☆】
1.運動の第1法則は加速度の法則である。
2.物体は静止を保ち続けようとする性質がある。
3.加速度は力の働く方向と同一方向に働く。
4.加速度は力の大きさに比例する。
答えと解説をみる
答え
1
1.加速度の法則は運動の第2法則です。
第1法則(慣性の法則)
1)静止している物体は外力が働かなければ、いつまでも静止している。
2)一様の運動をしている物体はいつまでも等速運動を続ける。
物体には運動や静止状態を保とうとする性質があります。
静止状態の関節に筋力という押し・引きの力が加わることにより運動が開始されます。
第2法則(加速度の法則)
1)加速度は力の大きさに正比例する。
2)加速度は物体の質量に反比例する。
3)加速度は力の働く方向と同一方向に働く。
加速度の法則は運動方程式(F=ma)で表されます。
a(加速度)、m(質量)、F(質量mの物体に加速度mを生じさせた力)
第3法則(作用・反作用の法則)
・物体Aが物体Bに力を作用させるとき、同時にBからもAに力を作用させている。
・この2つの力は同一作用線上で力の大きさが等しく、向きが逆。
・身体での適用例として徒手筋力検査法がある。
参考文献
・医歯薬出版「運動学 改訂第3版」




コメント